文章
的学习笔记
布隆过滤器(Bloom Filter),是 1970 年由布隆提出的,主要用于判断一个元素是否在一个集合中
传统集合储存元素的痛点是储存空间随元素个数线性增加,当数据量很多时,缺点便显现了出来,布隆过滤器解决了这一问题
原理
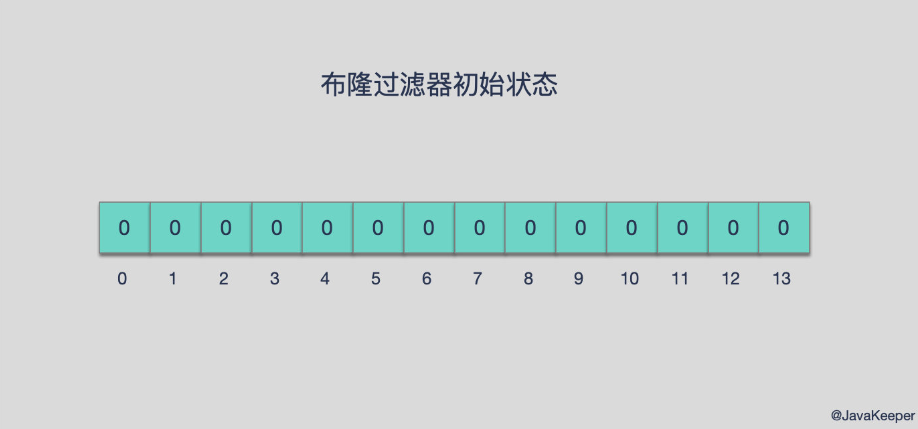
布隆过滤器的信息储存在固定大小的位图(Bitmap)中,初始时全为0
.
例如,两个对象经过三个哈希函数存储于布隆过滤器中如下图所示
.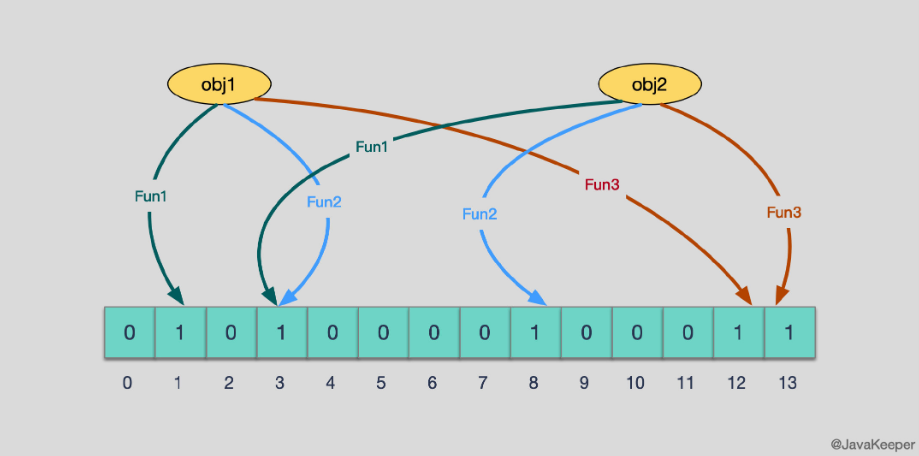
而且,由于哈希碰撞的存在, 布隆过滤器的查询也是有误判率存在的
优点:空间复杂度为$O(m)$,$m$为位图的宽度
缺点:
随着元素增多,误判率随之增加,因为布隆过滤器无法处理哈希碰撞
无法删除元素,因为如果把要删除的元素的所有位全置为0的话,就会影响到其他元素
要解决这一点,很自然的改进措施是在数组里储存计数器,删除元素时将计数器-1,但是由于哈希碰撞的存在,无法检测要删除的元素是否在容器中
特性:布隆过滤器并不保存元素本身,适合于保密等场景
参数选择
理论推导的误判率公式为
$$
p=[1-(1-\frac{1}{m})^{nk}]^k≈(1-e^{-\frac{kn}{m}})^k
$$
其中$n$为已经插入的元素数量
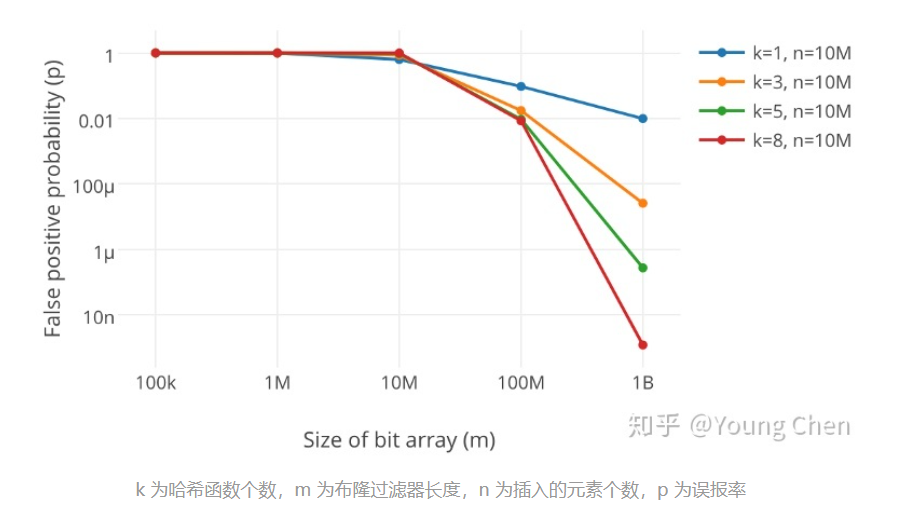
从公式可以分析出:
Bitmap宽度$m$:过大会占空间,过小会增大误判率
哈希函数个数$k$:过多会使Bitmap更快被填满(误判率在后期会升高),过小也会增大误判率
.
应用
业务场景:将用户已经浏览过的内容储存进布隆过滤器中,显然内容只增不减,这样就可以很方便地避免用户看到重复内容,当然,这会造成一些其他内容的误判,但无伤大雅
缓存穿透:
.
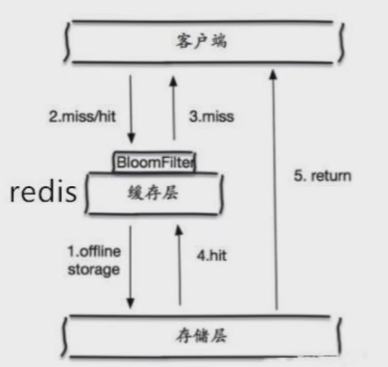
Web拦截,避免大量重复请求