WLQ's Blog
0%

HTTPS学习笔记

发表于 更新于 分类于

文章

的学习笔记

GET和POST的区别

GET POST
获取资源 提交数据
安全且幂等 不安全且不幂等

安全：不会破坏服务器资源

幂等：多次执行，结果相同

由于HTTP明文传输的特点，造成了以下三大危险

  • 窃听→加密：混合加密(对称AES+非对称RSA)
  • 篡改→校验：摘要算法
  • 冒充→证书

纯RSA+AES仍不安全

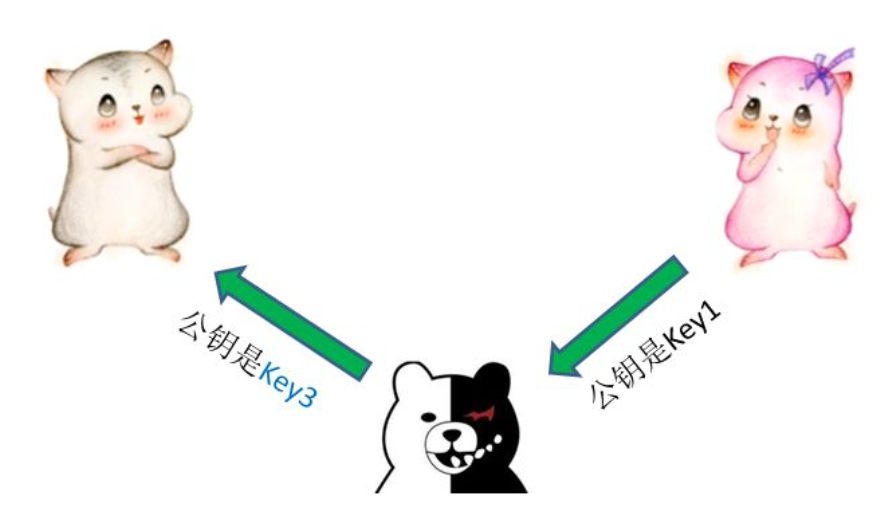
.image-20220316182644372

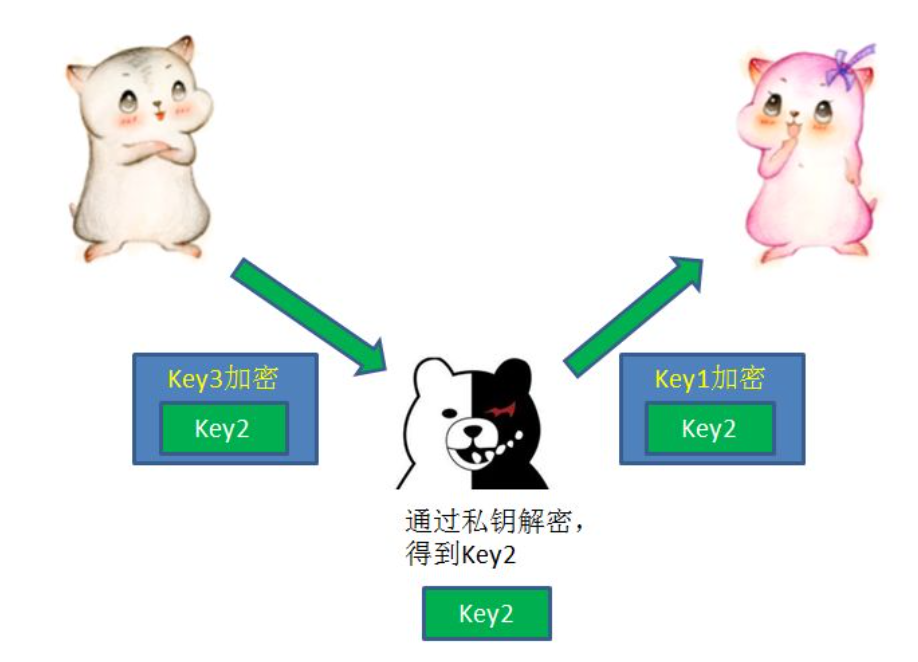
.image-20220316182727141

如此，中间人在双方都未意识到的情况下获得了AES密钥，因此需要第三方权威机构：CA

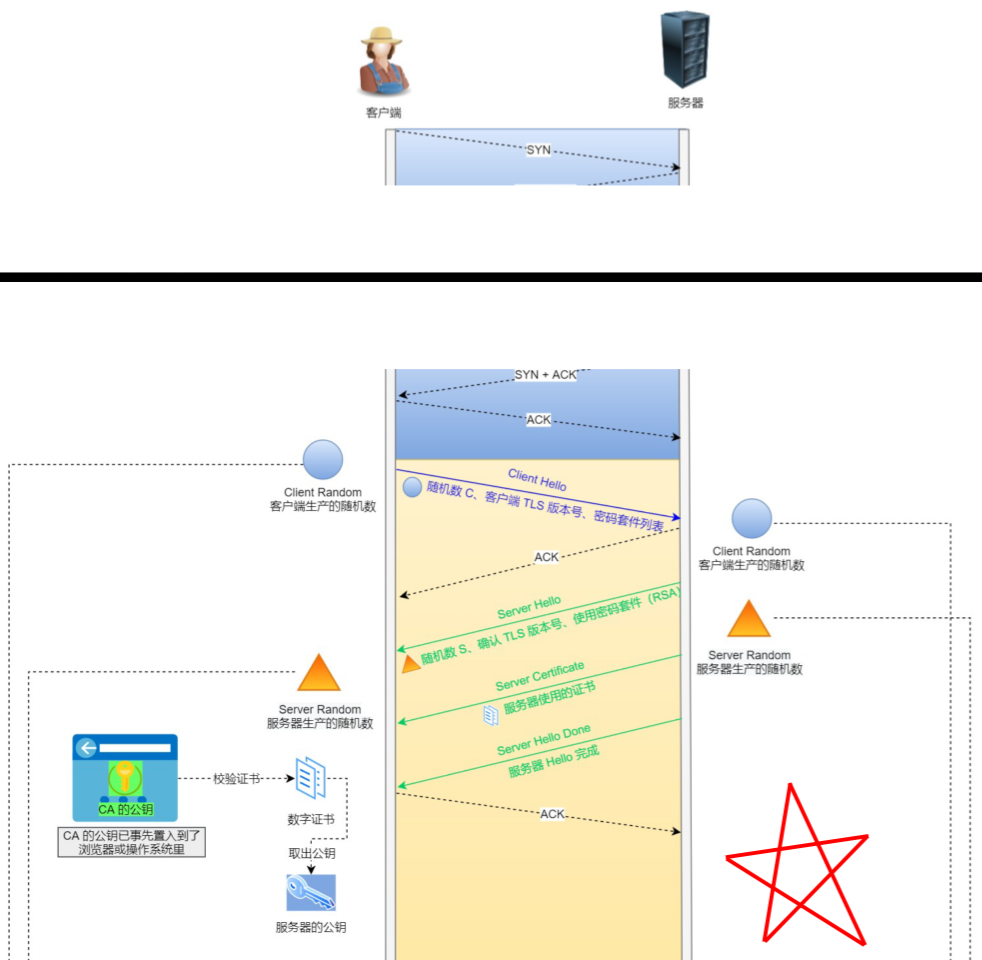
SSL/TLS加密的过程

TLS是SSL 3.0的升级版

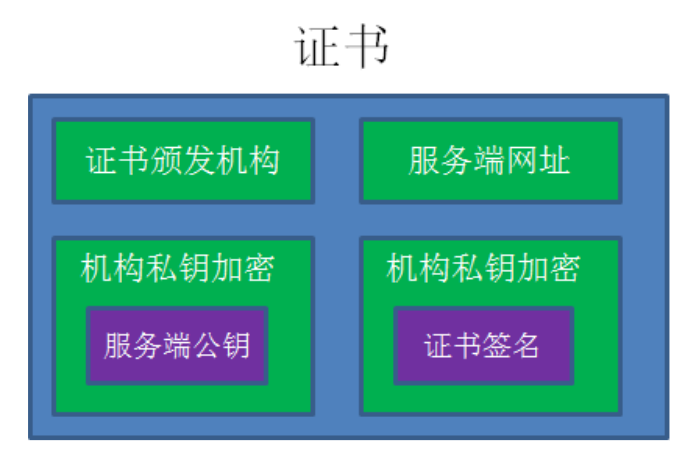
.image-20220316183113675

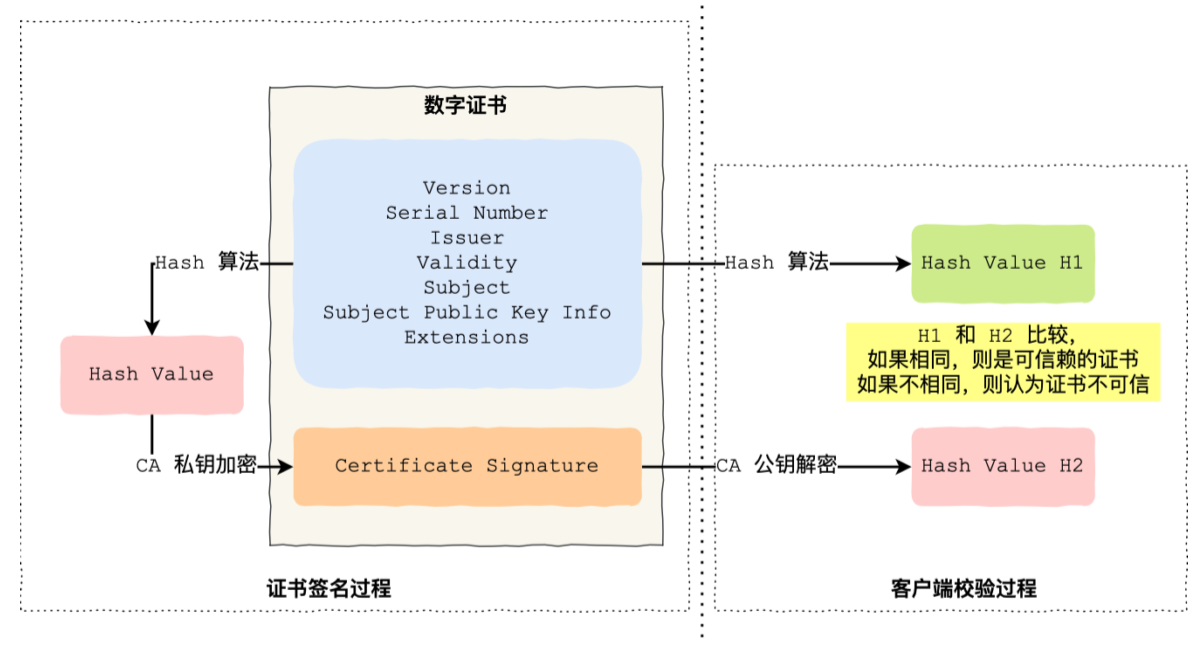
.image-20220316235455380

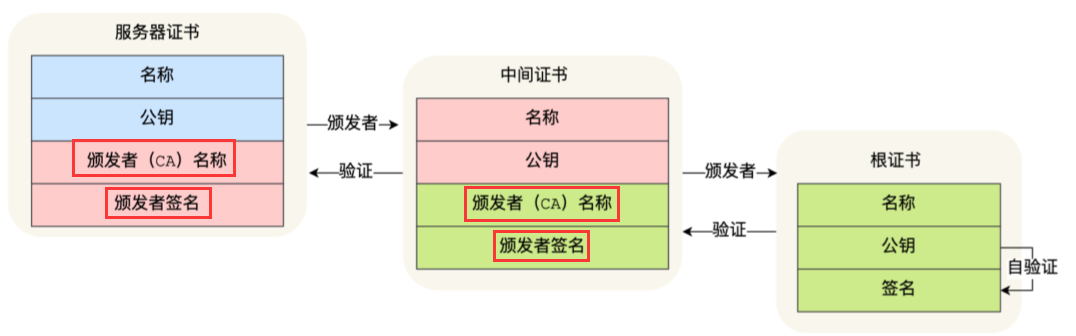
客户端拿到证书后，用CA公钥解密出签名，然后和自己生成的签名对比，若一致，则证书有效，然后用CA公钥解密取出服务器公钥

在这种情况下，中间人只能获取服务器公钥，但是无法篡改证书，进而无法获取AES密钥

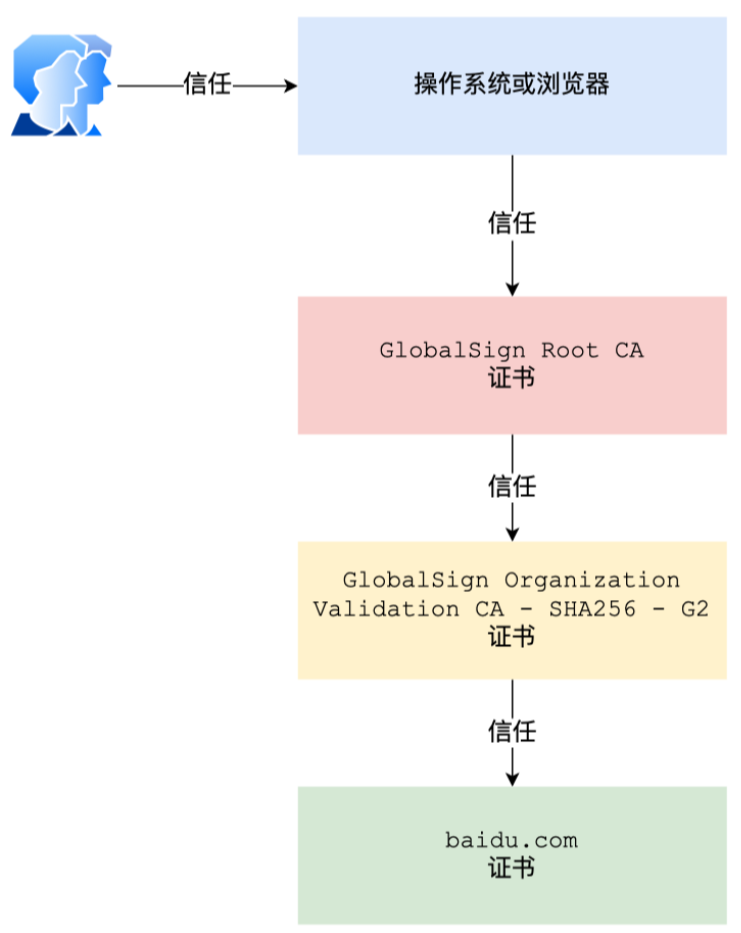
证书链：

.image-20220316235824049

.image-20220317000014509

.image-20220316213823825

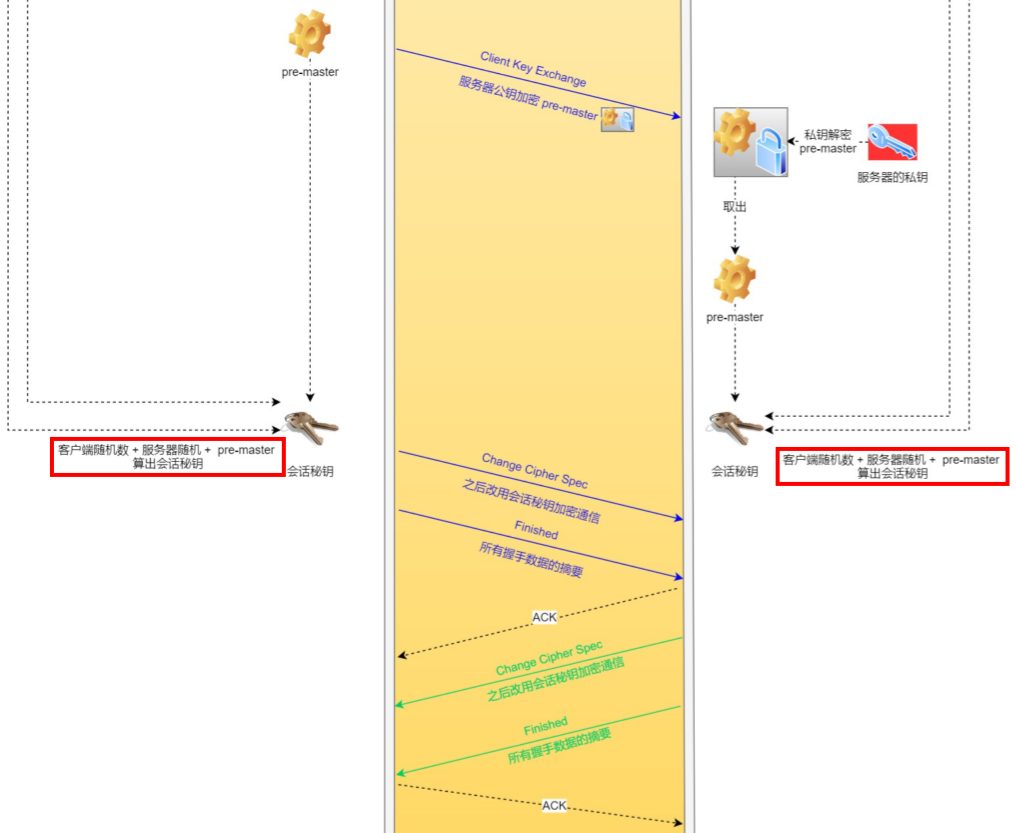
.image-20220316213906183

  • 先TCP，保证可靠性；再SSL/TLS，保证安全性
  • pre-master也是随机数，会话密钥由三个随机数生成
  • TLS/1.2一共4次握手(前3次生成随机数，后2次双重校验)
  • ACK表示“好的我收到了”

DH密钥交换算法

RSA算法不支持前向保密：一旦服务器的私钥泄露，之前发的所有TLS报文都会被破解(因为Pre-master被解密，而前两个随机数又是明文传输)

Diffie-Hellman密钥交换算法解决了这一问题

DH算法基于离散对数问题的困难性
$$
N^i\ mod\ P=K
$$
给定$N$和$P$，若知道$i$，求$K$很简单; 但若知道$K$，求$i$则很困难，尤其当$P$很大的时候，计算机无法算出离散对数

DH算法中，$N$和$P$作为公开的参数，$K$作为各自的公钥(记为$A$,$B$)，$i$作为各自的私钥(记为$a$,$b$)

可以证明
$$
A^b≡B^a\ (mod\ P)
$$
此即为对称加密密钥

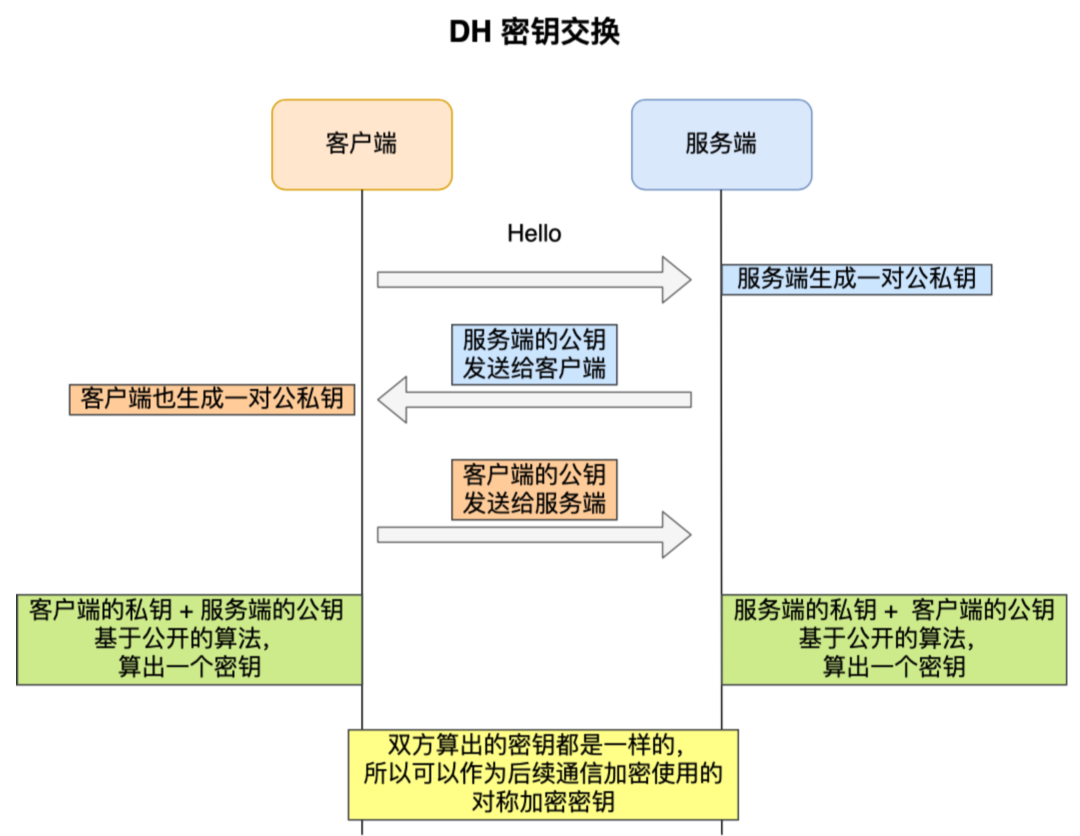
.image-20220317000741798

即使中间人截获了公钥，在不知道的私钥的情况下，无法计算出对称密钥，并且每次密钥都是实时⽣成的，实现了前向保密

ECDHE密钥交换算法

DH算法的计算效率很慢，ECDHE算法解决了这一问题，这也是大部分网站使用的算法

E意为Ephemeral(临时性的)，EC意为该算法利用ECC椭圆曲线特性，用更少的计算量计算出公钥和会话密钥

具体过程：

  1. 双方约定好椭圆曲线的种类，以及曲线上的一个基点$G$
  2. 双方各自生成随机数$d$(记为$d_1$和$d_2$)，公钥$Q=Gd$(记为$Q_1$和$Q_2$)
  3. 双方各自计算点$d_1Q_2$和点$d_2Q_1$，由于$d_1Q_2=d_1d_2G=d_2d_1G=d_2Q_1$，所以两点的**$x$坐标**相同

最终使用 「客户端随机数+服务器随机数+x坐标」生成最终的会话密钥

使用ECDHE握手，在TLS/1.2第四次握手前就已经可以发送HTTP报文，由2RTT降为1RTT

综上，ECDHE握手相比于RSA握手有三大优势：前向保密+计算效率高+提前发送HTTP报文