WLQ's Blog
0%

平衡树

发表于 更新于 分类于

本文总结了三种平衡树：B+树、红黑树、AVL树

B+树

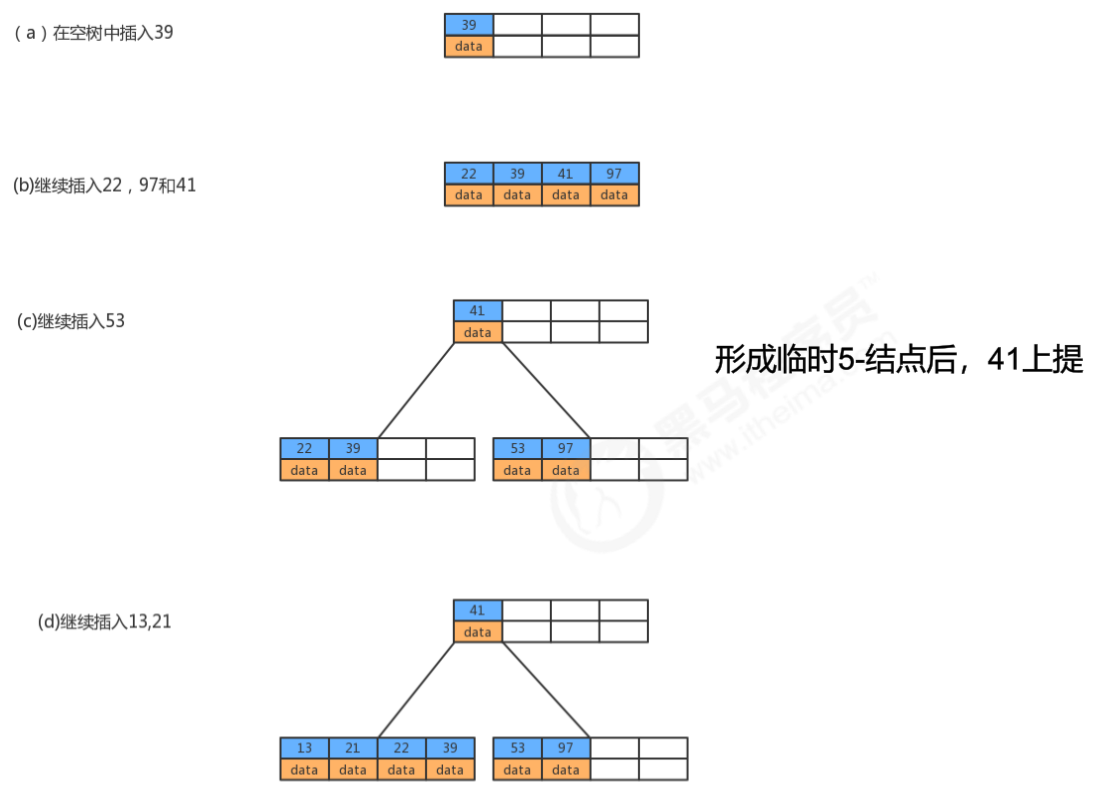
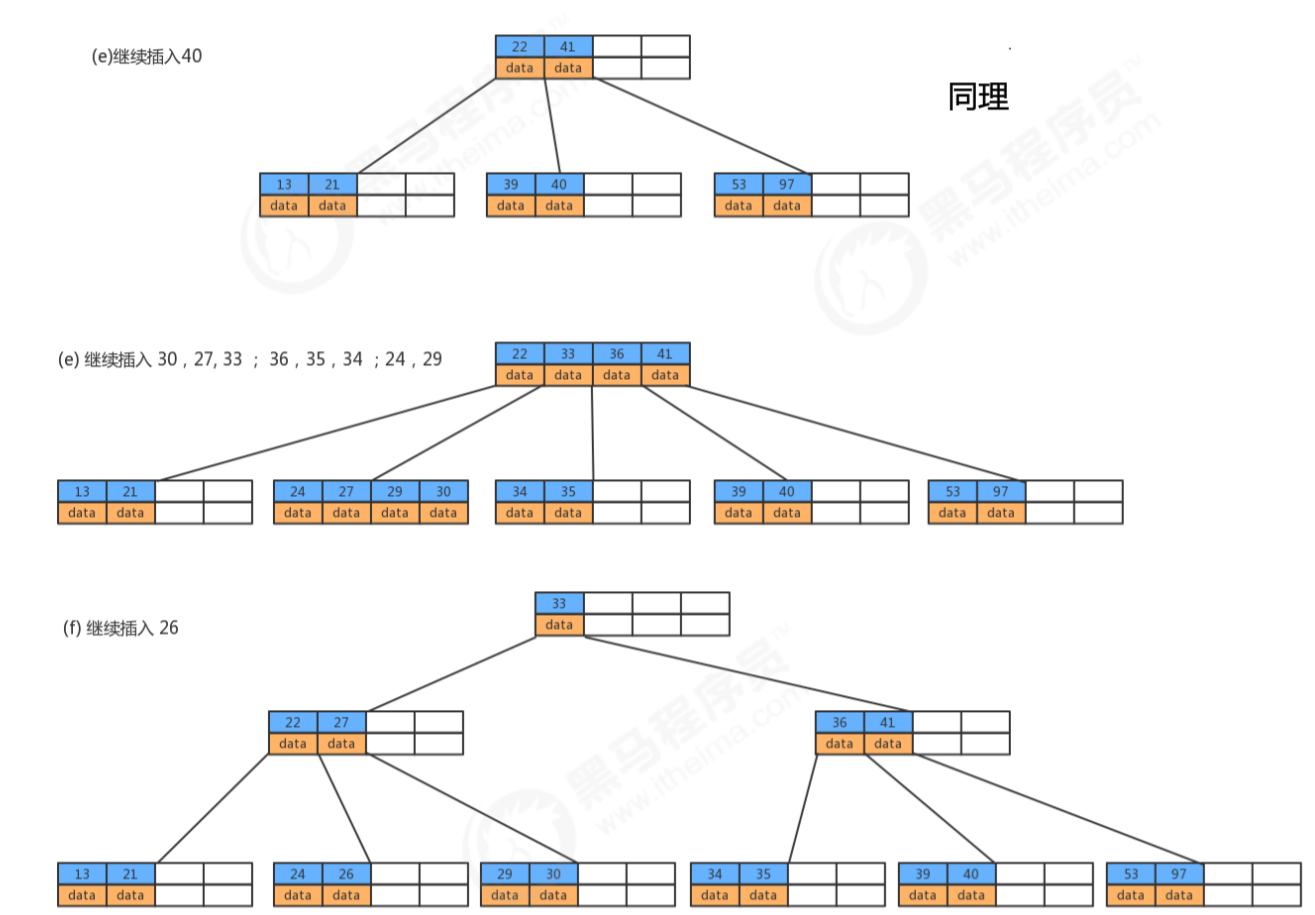
  • B树应用：磁盘上的文件

.image-20220212223541736

.image-20220212223611051

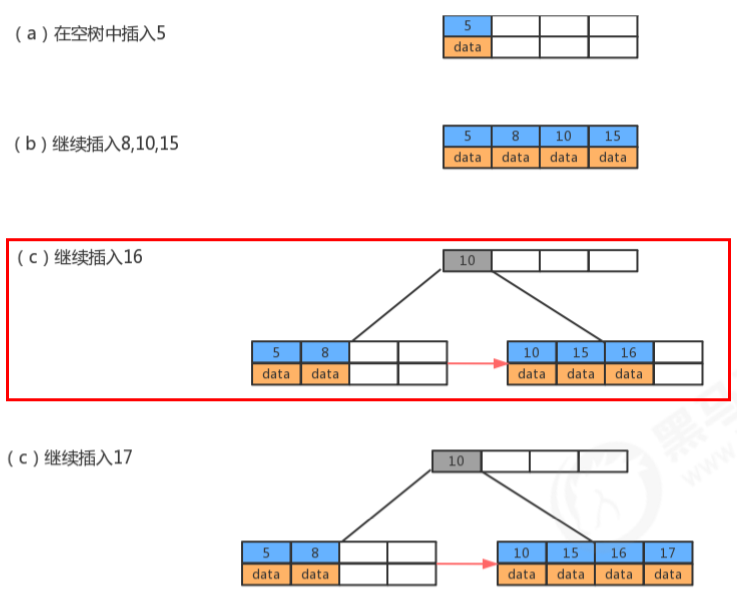
  • B+树

.image-20220212223801036

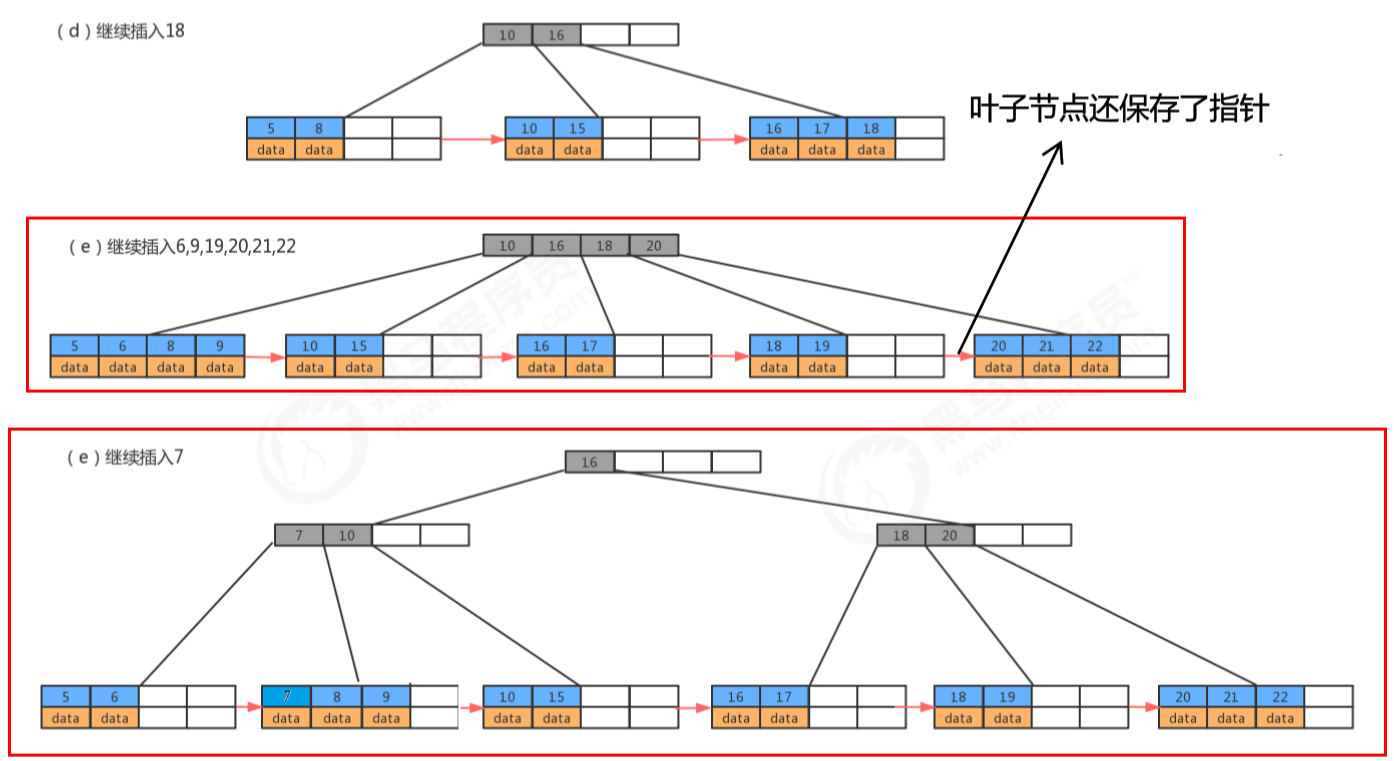
image-20220212223936458

红黑树

参考资料

HashMap的红黑树是2-3-4红黑树，而不是2-3红黑树，这里讨论2-3-4红黑树

红黑树确保从根到叶子的最长路径不会超过最短路径的2倍

一颗有$n$个结点的红黑树，高度至多为$2log(n+1)$

  • 根节点必为黑色
  • 完美黑色平衡：任意节点到叶子节点经过的黑色节点数目相同。因为只有黑节点会贡献高度，而且2-3-4树的叶节点到根节点距离相同
  • 红节点的子节点为黑色
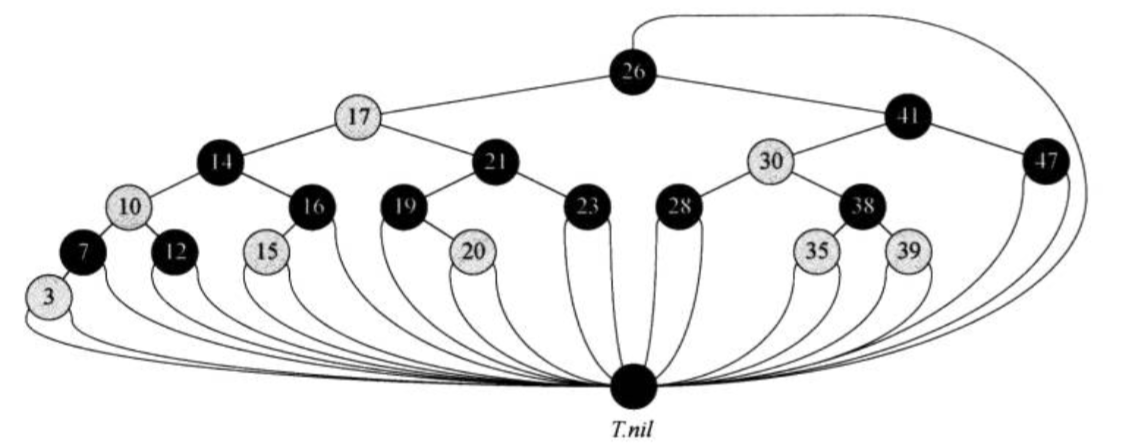
image-20220213223214805

红节点永远是结合黑节点的，黑节点永远是连接其他结点的

image-20220213223345511

插入

先像BST一样插入（插入的结点染成红色），再调平

z的父若为黑(2结点被结合为3结点)，则不用调平。所以以下情况z的父必为红

case0: z为根结点

将z变为黑色即可

case1: z的叔为红

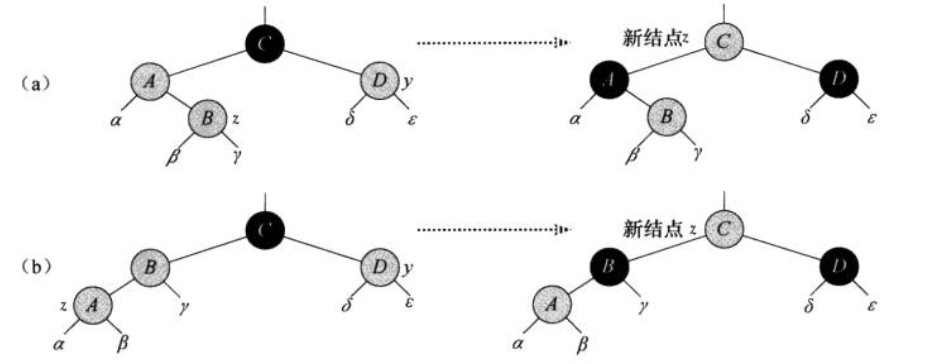
.image-20220213224610708

进行颜色转换，并将C视为新插入的结点，继续调平

相当于一个5结点分裂，C结点上提(C结点变红与其他节点结合)

case2: z的叔为黑，z是右孩子

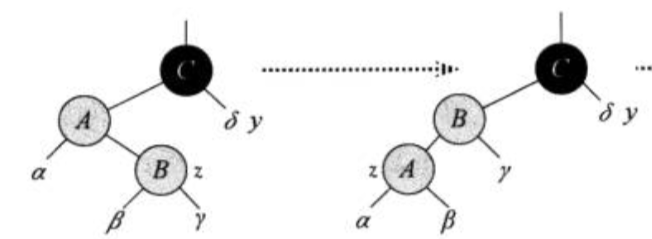
.image-20220213230041412

进行左旋(对称情况为右旋)，变为case3

3结点被结合为4结点，并没有分裂

case3: z的叔为黑，z是左孩子

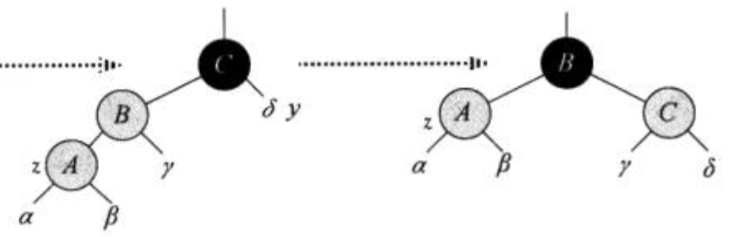
.image-20220213225913974

进行右旋(对称情况为左旋)

3结点被结合为4结点，并没有分裂

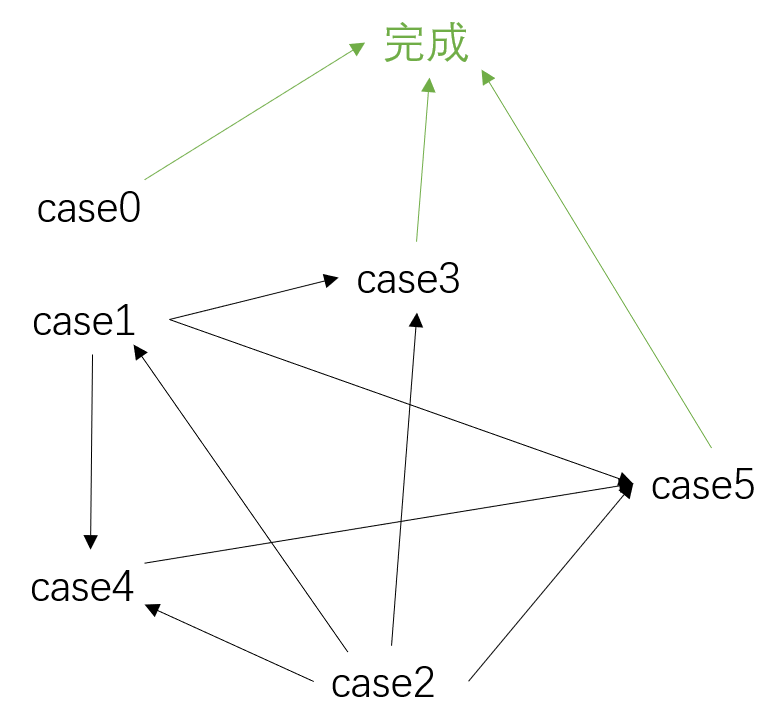
状态转移图

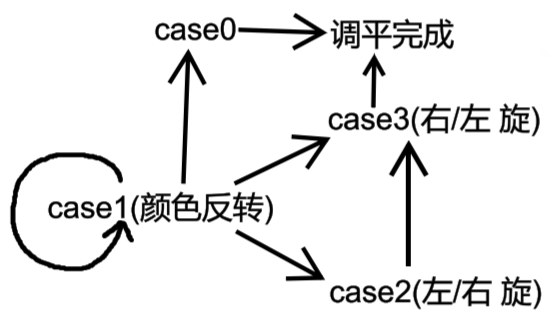
.image-20220213233204832

一旦走出case1就标志着结束

删除

先像BST一样删除，再调平

BST删除

case1: 没有子节点 & 只有一个子节点

直接将子节点移植到该节点

case2: 有两个子节点

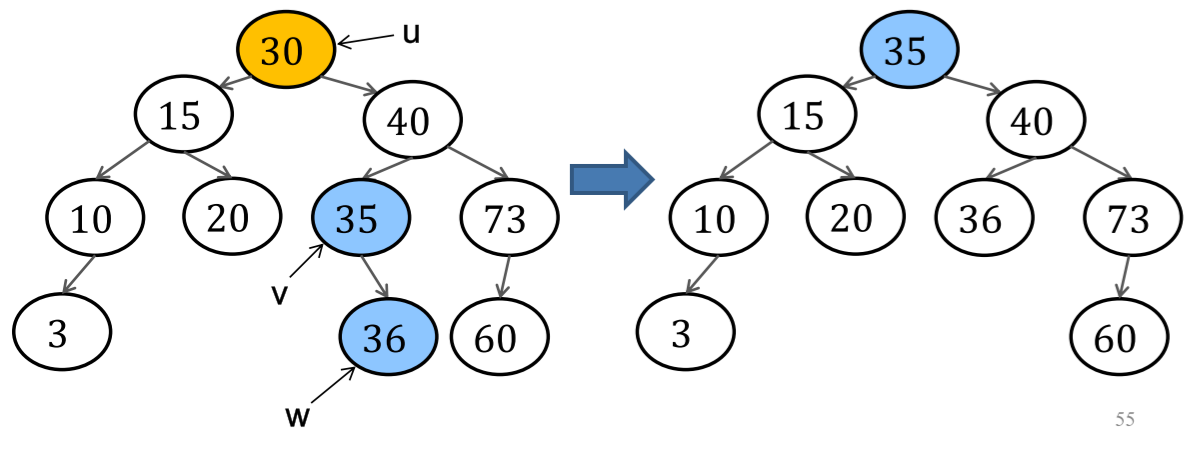
.image-20220214093910099

找到后继节点v，进行替换。然后按case1删除v

调平

注意：红黑树中的BST删除只改变值，而不改变颜色！

经过替换，最终删除的一定是2-3-4树的最底层

可以发现，若最终删除的是红节点，则不用调平，最终的删除是实实在在的删除，而不是只替换值

删除结点为黑色时，整棵树的黑高-1，需要调平

case0: 子节点为红

直接将子节点染成黑色即可修复

所以，以下分类仅针对“删除节点和子节点均为黑”的情况，N是删除后被替换的结点

记忆：case1~case3兄的子均为黑

case1: 只有兄为红

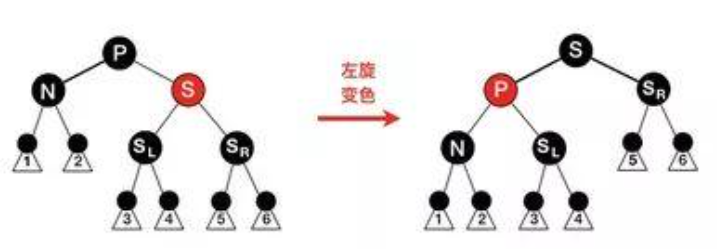
.image-20220214210408438

左旋，黑高仍未调平，转变为其他情况(N=N)

case2: 全为黑

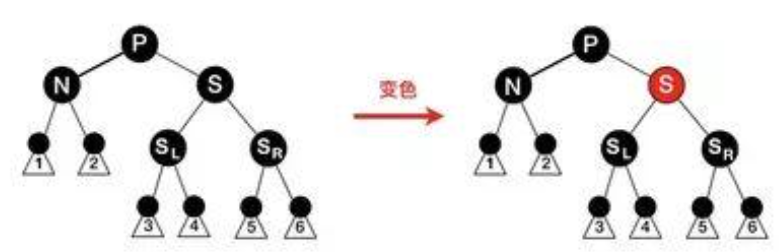
.image-20220214210640197

只改变兄结点的颜色，则三条路径黑高均-1，转变为其他情况(N=P)

case3: 只有父为红

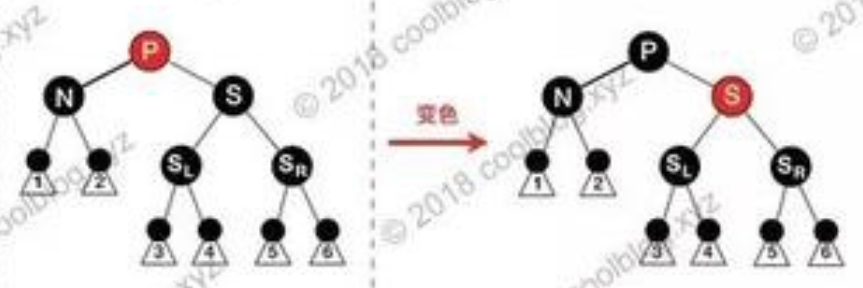
.image-20220214213222926

交换兄父颜色，因为N结点黑高+1，所以修复完成

case4: 兄为黑，兄左为红，兄右为黑

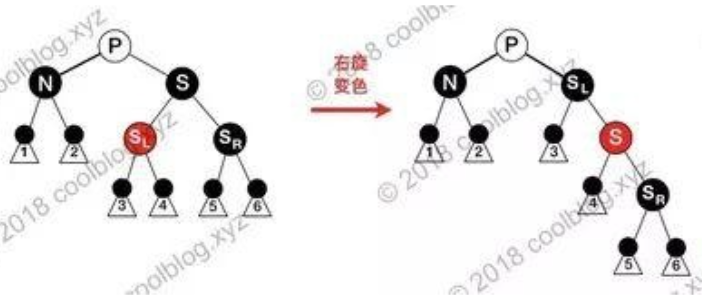
.image-20220214213931293

对S右旋，转变为case5

case5: 兄为黑，兄右为红

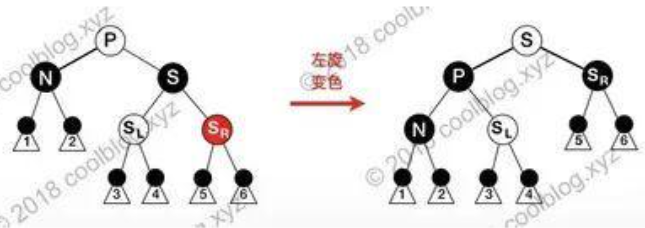
.image-20220214214216214

对P左旋，因为N结点黑高+1，修复完成

对称同理

.image-20220214215919058

.image-20220213223214805

实际上，由于最终删除的是最底层，几乎无法出现case1~case5的情况

AVL树

定义：所有结点的左右子树高度相差不超过1

经过BST插入和删除后，需要调平

注意，调整的是【最底部】的不平衡结点

left-left case

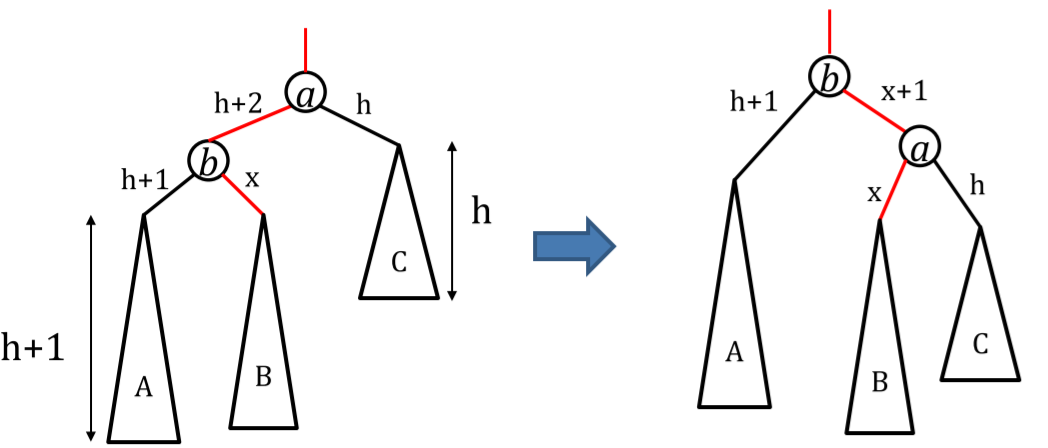
.image-20220214224302912

右旋

left-right case

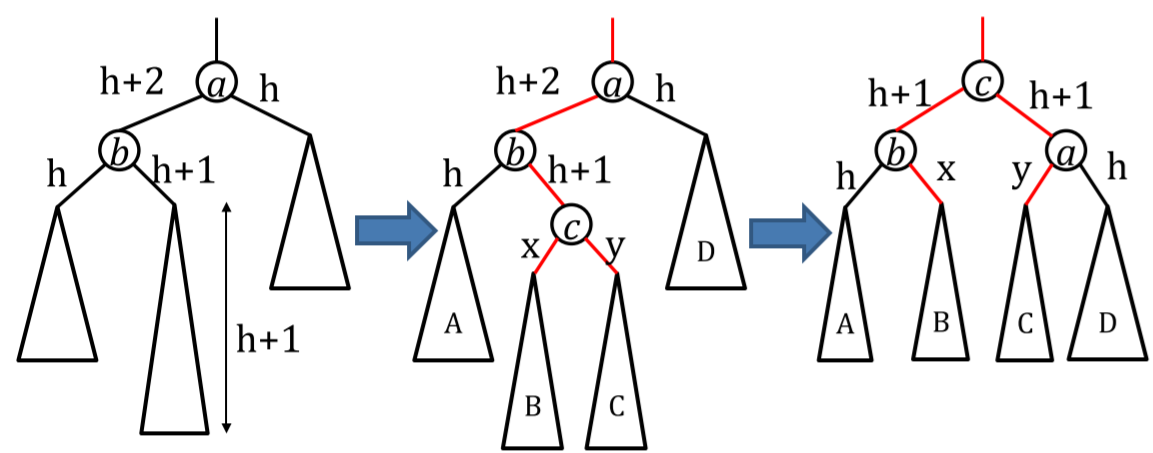
.image-20220214224454600

对称情况同理

HashMap为什么选红黑树而不是AVL树？

平衡度 调整频率 适用场景
AVL树 高 高 查询多，增删少
红黑树 低 低 增删频繁